Simple Harmonic motion

Defining equation

displacement, velocity and acceleration

Kinetic and potential energy

Energy transfer

Period of pendulum and mass-spring

Single-slit diffraction

What is single slit diffraction

Diffraction: a wave phenomena that occurs when a wave comes in contact with an obstacle or a slit. 

Single slit diffraction describes how a wave passing through a slit is bent upon exiting the slit. When this new curved wave hits a wall, a single-slit diffraction pattern is seen.

The single pattern is described by:

• A bright central maximum intensity
• Other smaller maxima on either side (about 20% of maximum intensity)
• Central fringe is twice as wide as other fringes

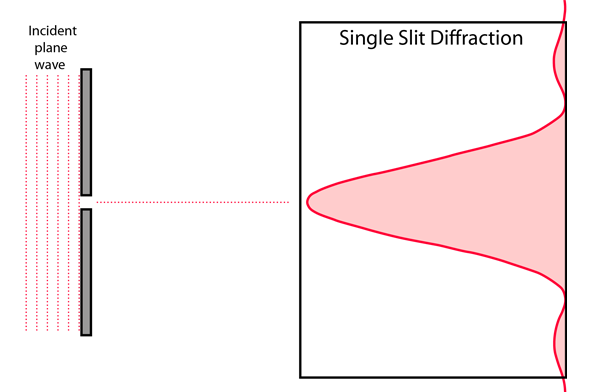
Single slit diffraction pattern explained

The shape and intensity plot of single slit diffraction is caused by an idea known as Huygens' principle. This principle says that at every point on an advancing wave front acts as the center of a new wavelet emanating from that point. Thus we can consider the slit has having a infinite number of secondary wave sources which can constructively and destructively interfere with each other, as shown below. 

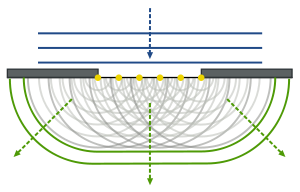
Explanation of central maximum and first minimum

Because the distance between the screen and slit is so big compared to the size of the slit, the angle between a specific point on the screen and any secondary source is approximately equal. 

• In the forward direction the angle is zero, which means that as every secondary has the same angle all have the same path difference. This causes constructive interference and there will be a maximum at the center. (This is a bit simplified but the real answer would only confuse you)
• Moving out from the center, there is more and more destructive interference, and the intensity falls
• At a specific point it can be shown that the path difference between a secondary source at the edge and at the center is \(\frac{\lambda}{2}\) and so there is destructive interference resulting in zero intensity. By pairing off every point in the upper half of the slit with on in the lower half, and showing each also has a path difference of \(\frac{\lambda}{2}\), it can proved that at this point there will be an intensity of 0. This is the first minimum.
• In order to identify a clear diffraction pattern, the light incident upon the slit must be monochromatic and coherent.

Single-slit diffraction formula

\(\theta = \frac{\lambda}{b} = \frac{wavelength}{slit diameter}\)

derivation of single slit equation

Since the first minimum is at a point where the path difference between to parallel paths is \(\frac{\lambda}{2}\), we can determine a relationship between the angle from the center, \(\lambda\) and b.

• Using trigonometry we get that \(sin\theta = \frac{lambda}{b}\)
• Since \(\theta\) is very small we can say that \(sin\theta \approx \theta\)
• This gives \(\theta = \frac{lambda}{b}\)

Effect of slit width on single slit diffraction

• From the equation \(\theta = \frac{\lambda}{b}\) we know that as the slit width decreases the angle gets bigger meaning the intensity plot spreads out more
• If the slit is smaller less light is let through and the maximum intensity is less.

Single slit diffraction with white light

White light is a combination of different wavelengths and so when it is incident with a single slit, each wavelength of light will have it's own interference pattern. 

• The longer the wavelength the more spread out the interference pattern, the shorter the wavelength the more narrow the interference pattern
• This means when white light passes through a slit it will create rainbow pattern, with the longer wavelengths of light on the outsides and the shorter wavelengths closer to the center.
• The maximum intensity is at the center no matter the wavelength so the first maximum will still be a white fringe.

Young's double slit Interference

Modulation of two-slit interference pattern by one-slit diffraction effect

Multiple slit diffraction

Multiple Slit Basics

When the number of slits is increased (and constant spacing between slits is maintained), there are two resulting effects:

1. Bright fringes maintain their place but become narrower (sharper)
2. The intensity of the bright fringes increases (proportional to N²). This means that an experiment with a 5-slit arrangement will have an intensity 25 times higher than a single slit arrangement. The fringe pattern stays within the single-slit diffraction envelope. 

With patterns with 3 or more slits, subsidiary fringes (less intense, secondary peaks) will develop. The number of subsidiary fringes is equal to N - 2, where N is the number of slits. 

Diffraction Grating

Diffraction Grating: A large number (hundreds to even thousands) of equally spaced, parallel, small slits, often in glass or plastic. They are described by the number of lines per millimeter.

Calculate the distance between the slits: d (in m)= .001/(number of lines per mm)

White light on the grating will cause a series of spectra to form, similar to maxima. Each group of spectra is called an order and is numbered in the same way as maxima. 

The diffraction-grating equation: nλ = dsinθ_n, 

Where:

• n is the order
• λ is the wavelength
• d is the grating spacing
• θ is the angle between the central maximum and the order's maximum

Thin film interference

Resolution

The size of a diffracting aperture

Resolution and Rayleigh criterion 

Resolvance of diffraction gratings

Doppler effect

Doppler effect for sound and light waves

Situations involving doppler effect

Determining velocity

View count: 4389